Writing an Intepreter in Rust

When I first picked up Thorsten Ball's excellent book "Writing an Interpreter in Go", I knew I wanted to tackle the challenge of implementing the Monkey programming language. However, instead of following along in Go, I decided to take the opportunity to improve on my Rust!
What is Monkey?
Monkey is a C-like programming language designed specifically for learning about interpreters and language implementation. It includes:
- Variable bindings:
let x = 5; - Integers and booleans:
42,true,false - Arithmetic expressions:
+,-,*,/ - Built-in functions:
len(),first(),last(),rest(),push() - First-class functions: Functions are values that can be passed around
- Higher-order functions: Functions that take other functions as arguments
- Closures: Functions that capture their environment
Here's a taste of what Monkey looks like:
// Fibonacci function with closures
let fibonacci = fn(x) {
if (x == 0) {
0
} else {
if (x == 1) {
1
} else {
fibonacci(x - 1) + fibonacci(x - 2)
}
}
};
fibonacci(10); // => 55Architecture Overview
My Rust implementation follows the classic interpreter architecture with three main components:
- Lexer - tokenizes the source code
- Parser - builds an Abstract Syntax Tree (AST)
- Evaluator - walks the AST and executes the program
1. Lexer
The lexer converts a stream of characters into tokens—the first step in understanding any program. Think of it as breaking down a sentence into individual words and punctuation marks, but for code.
The core responsibility is simple: define your set of supported tokens, scan through your program character by character, and output a list of tokens that the parser can work with. Here's how I defined the token types in my implementation:
#[derive(Debug, PartialEq, Clone)]
pub enum Token {
Ident(String),
Integer(i32),
True,
False,
Illegal,
Eof,
Equal,
Plus,
Comma,
Semicolon,
LParen,
RParen,
LBrace,
RBrace,
Function,
Let,
Assign,
Bang,
Dash,
ForwardSlash,
Asterisk,
NotEqual,
LessThan,
GreaterThan,
Return,
If,
Else,
}Rust's enum system was perfect for representing tokens with values (like Ident(String) and Integer(i32)). This made my Lexer implementation extremely simple:
impl Lexer {
pub fn next_token(&mut self) -> Token {
self.skip_whitespace();
let tok = match self.cur_char {
b'{' => Token::LBrace,
b'}' => Token::RBrace,
b'(' => Token::LParen,
b')' => Token::RParen,
b',' => Token::Comma,
b';' => Token::Semicolon,
b'+' => Token::Plus,
b'-' => Token::Dash,
b'!' => {
if self.peek_char() == b'=' {
self.read_char();
Token::NotEqual
} else {
Token::Bang
}
},
b'>' => Token::GreaterThan,
b'<' => Token::LessThan,
b'*' => Token::Asterisk,
b'/' => Token::ForwardSlash,
b'=' => {
if self.peek_char() == b'=' {
self.read_char();
Token::Equal
} else {
Token::Assign
}
},
0 => Token::Eof,
c => {
if Self::is_letter(c) {
let id = self.read_identifier();
return match id.as_str() {
"fn" => Token::Function,
"let" => Token::Let,
"true" => Token::True,
"false" => Token::False,
"if" => Token::If,
"else" => Token::Else,
"return" => Token::Return,
_ => Token::Ident(id),
};
} else if c.is_ascii_digit() {
let id = self.read_number();
return Token::Integer(id);
} else {
Token::Illegal
}
}
};
self.read_char();
return tok;
}
}
Reading tokens became a simple matter of using pattern matching, incrementing your current cursor position.
2. Parser
Now that we have a sequence of input tokens, we can build our parser which takes input tokens and converts them into a data structure representation, most typically an Abstract Syntax Tree (AST). This tree structure represents the hierarchical syntax of the program in a way that will make it easy for our evaluator to traverse.
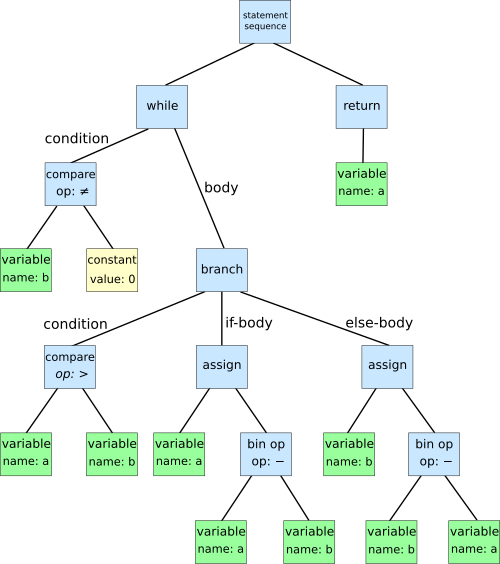
We implement a Recursive Descent Parser, commonly known as a Top-Down Operator Precedence parser or Pratt Parser. This approach starts at the root node of the AST and descends down, mirroring how we naturally think about ASTs. While it's not the fastest parsing method and lacks formal proof of correctness, it's the easiest to learn and implement.
I defined the AST nodes using enums and structs:
#[derive(Debug, Clone)]
pub enum Statement {
Let(String, Expression),
Return(Expression),
Expr(Expression),
}
#[derive(Debug, Clone)]
pub enum Expression {
Ident(String),
Lit(Literal),
Prefix(Token, Box<Expression>),
Infix(Token, Box<Expression>, Box<Expression>),
If(Box<Expression>, BlockStatement, Option<BlockStatement>),
Function(Vec<String>, BlockStatement),
FunctionCall(Box<Expression>, Vec<Expression>),
}Statements
Parsing statements is relatively straightforward, we process tokens from left to right, expect or reject the next token, and if it matches our expectations, we return an AST node. A typical let statement let x = a + b;for example:
fn parse_let_statement(&mut self) -> Result<Statement, ParserError> {
let ident = match &self.peek_token {
Token::Ident(id) => id.clone(),
t => {
return Err(self.error_no_identifier(t));
}
};
// Consume identifier
self.next_token();
self.expect_peek_token(&Token::Assign)?;
self.next_token();
let expr = self.parse_expression(Precedence::Lowest)?;
if self.peek_token_is(&Token::Semicolon) {
self.next_token();
}
Ok(Statement::Let(ident, expr))
}Expressions & Pratt Parsing
The real challenge comes with parsing expressions! Even with a simple example like: 2 + 3 * 4 where operator precedence and associativity matter. This is where Top-Down Operator Precedence (Pratt Parsing) shines. The elegance of Pratt parsing lies in its simplicity and extensibility:
- Single parsing function: One
parse_expressionfunction handles all precedence levels - Natural handling of associativity: Left vs right associativity is handled by a simple precedence adjustment
- Easy to extend & readable: Adding new operators requires just updating the precedence table and adding cases. The parsing logic directly reflects the mathematical properties of operators
It took me a while to understand this concept fully—most of the implementation closely follows the patterns from the book. At a high level, Pratt Parsing follows high-level recursive algorithm:
fn parse_expression(&mut self, precedence: Precedence) -> Result<Expression, ParserError> {
// Parse the left side (prefix)
let mut left_exp = self.parse_prefix_expression()?;
// Continue parsing infix operators while they have higher precedence
while !self.peek_token_is(&Token::Semicolon) && precedence < self.next_token_precedence() {
left_exp = self.parse_infix_expression(left_exp)?;
self.next_token();
}
Ok(left_exp)
}
Let's trace how this parser handles 2 + 3 * 4 to see the magic in action:
- Start:
parse_expression(Precedence::Lowest) - Parse prefix: Consumes
2, returnsLiteral::Integer(2) - Check infix: Current token is
Pluswith precedence 1 ≥ 0, so continue - Parse infix:
- Consumes
Plus - Calls
parse_expression(2)for right side (precedence + 1) - Nested call:
- Parse prefix: Consumes
3, returnsLiteral::Integer(3) - Check infix: Current token is
Multiplywith precedence 2 ≥ 2, so continue - Parse infix: Consumes
Multiply, callsparse_expression(3)- Parse prefix: Consumes
4, returnsLiteral::Integer(4) - Check infix: EOF has precedence 0 < 3, so stop
- Returns
Expression::Infixwith*operator
- Parse prefix: Consumes
- Returns
Expression::Infixwith+operator
- Parse prefix: Consumes
- Consumes
The result is the correctly structured AST: +(2, *(3, 4)) which respects operator precedence!
Although tracing through examples made sense during implementation, it didn't offer me an intuitive explanation of how it worked. I found Alex Kladov's explanation to be more understandable. You can think of precedence as 'binding power'. Operatators like * have higher precedence and binding power than + and will hold their operands closer.
expr: A + B * C
power: 3 3 5 5Since we implemented a left to right parser, when you have operators with the same precedence, operands on the right will have slightly higher power
expr: A + B + C
power: 0 3 3.1 3 3.1 0So now the first operand will group its expression first leading to (A + B) + C.
My final implementation:
#[derive(Debug, PartialEq, PartialOrd)]
pub enum Precedence {
Lowest,
Equals, // == or !=
LessGreater, // > or <
Sum, // + or -
Product, // * or /
Prefix,
Call,
}
impl Parser {
fn parse_expression(&mut self, precedence: Precedence) -> Result<Expression, ParserError> {
let mut left_expr = match self.current_token {
Token::Ident(ref id) => Ok(Expression::Ident(id.clone())),
Token::Integer(i) => Ok(Expression::Lit(Literal::Integer(i))),
Token::True => Ok(Expression::Lit(Literal::Boolean(true))),
Token::False => Ok(Expression::Lit(Literal::Boolean(false))),
Token::Bang | Token::Dash => self.parse_prefix_expression(),
Token::LParen => {
self.next_token();
let expr = self.parse_expression(Precedence::Lowest);
self.expect_peek_token(&Token::RParen)?;
expr
},
Token::If => self.parse_if_expression(),
Token::Function => self.parse_fn_expression(),
_ => {
return Err(ParserError::new(format!(
"No prefix parse function for {} is found",
self.current_token
)));
}
};
while !self.peek_token_is(&Token::Semicolon) && precedence < self.next_token_precedence() {
match self.peek_token {
Token::Plus
| Token::Dash
| Token::Asterisk
| Token::ForwardSlash
| Token::Equal
| Token::NotEqual
| Token::LessThan
| Token::GreaterThan => {
self.next_token();
let expr = left_expr.unwrap();
left_expr = self.parse_infix_expression(expr);
}
Token::LParen => {
self.next_token();
let expr = left_expr.unwrap();
left_expr = self.parse_fn_call_expression(expr);
}
_ => return left_expr,
}
}
left_expr
}
pub fn next_token_precedence(&self) -> Precedence {
match &self.peak_token {
Token::Asterisk | Token::ForwardSlash => Precedence::Product,
Token::Plus | Token::Dash => Precedence::Sum,
Token::LessThan | Token::GreaterThan => Precedence::LessGreater,
Token::Equal | Token::NotEqual => Precedence::Equals,
Token::LParen => Precedence::Call,
_ => Precedence::Lowest,
}
}
}
Again, Rust's pattern matching made this implementation clean and easy to write. One of the biggest challenges was managing ownership in the recursive AST structure. Boxing expressions (Box<Expression>) solved the recursive type issue, and cloning where necessary kept the borrow checker happy while maintaining clean code.
3. Evaluation
The evaluator is where our Monkey programs will come to life. implemented a tree-walking interpreter, a straightforward approach that traverses the AST and executes code by recursively visiting each node and performing the associated operation. The core concept is beautifully simple. For each AST node, we:
- Examine the node type
- Recursively evaluate child nodes if needed
- Perform the operation specific to that node type
- Return the result
Here's the basic algorithm in pseudocode:
function eval(astNode) {
if (astNode is integerLiteral) {
return astNode.integerValue
} else if (astNode is booleanLiteral) {
return astNode.booleanValue
} else if (astNode is infixExpression) {
leftEvaluated = eval(astNode.Left)
rightEvaluated = eval(astNode.Right)
if astNode.Operator == "+" {
return leftEvaluated + rightEvaluated
} else if astNode.Operator == "-" {
return leftEvaluated - rightEvaluated
}
}
}
Let's trace through evaluating (5 + 3) * 2:
- Start:
eval(InfixExpression { "*", left: InfixExpression { "+", 5, 3 }, right: 2 }) - Evaluate left operand:
eval(InfixExpression { "+", 5, 3 })- Evaluate left:
eval(5)→Object::Integer(5) - Evaluate right:
eval(3)→Object::Integer(3) - Apply operator:
5 + 3→Object::Integer(8)
- Evaluate right operand:
eval(2)→Object::Integer(2)
- Apply main operator:
8 * 2→Object::Integer(16)
The beauty is that each recursive call handles exactly one level of the tree, making the algorithm both simple to understand and implement.
My final implementation looked something like:
fn eval_expression(expr: &Expression, env: &Env) -> Result<Object, EvalError> {
match expr {
Expression::Ident(id) => eval_identifier(&id, env),
Expression::Lit(lit) => eval_literal(lit),
Expression::Prefix(op, expr) => {
let right = eval_expression(expr, env)?;
eval_prefix_expression(op, &right)
},
Expression::Infix(op, left, right) => {
let left = eval_expression(left, &Rc::clone(env))?;
let right = eval_expression(right, &Rc::clone(env))?;
eval_infix_expression(op, &left, &right)
},
Expression::If(condition, consequence, alternative) => {
let condition = eval_expression(condition, &Rc::clone(env))?;
if is_truthy(&condition) {
eval_block_statement(consequence, env)
} else {
match alternative {
Some(alt) => eval_block_statement(alt, env),
None => Ok(Object::Null),
}
}
},
Expression::Function(params, body) => Ok(Object::Function(
params.clone(),
body.clone(),
Rc::clone(&env),
)),
Expression::FunctionCall(func, args) => {
let func = eval_expression(func, &Rc::clone(env))?;
let args: Result<Vec<Object>, EvalError> = args.iter().map(|arg| eval_expression(arg, env)).collect();
apply_function(&func, &args?)
}
_ => Err(EvalError::new(format!(
"unknown expression: {}",
expr
))),
}
}
The most challeging portion of implement the evaluation algorithm was handling function calls and closures. This required the introduction of environment management, where I learned a useful patterns for handling shared, mutable state in Rust.
Shared Mutable References
In languages with garbage collection, you might simply store a reference to the parent environment. But Rust's ownership system doesn't allow multiple mutable references to the same data. Consider this Monkey code:
let makeCounter = fn() {
let count = 0;
fn() {
count = count + 1;
count
}
};
let counter1 = makeCounter();
let counter2 = makeCounter();
counter1(); // => 1
counter1(); // => 2
counter2(); // => 1 (independent counter)
Each closure needs to:
- Share the same environment with its parent scope
- Mutate variables in that shared environment
- Outlive the function that created it
The Rc<RefCell<T>> pattern solves this by combining two powerful Rust concepts. Rc<T> allows shared, immutable access of data to multiple owners to the same data and automatically deallocates when the last reference is dropped. RefCell<T> provides interior mutability (mutation through shared references) and moves borrow checking from compile-time to runtime. Using this pattern, I implemented the environment management, which was essentially a nested hashmaps of each closure's objects:
use crate::object::*;
use std::collections::HashMap;
use std::rc::Rc;
use std::cell::RefCell;
pub type Env = Rc<RefCell<Environment>>;
#[derive(Debug, Default, Clone)]
pub struct Environment {
store: HashMap<String, Rc<Object>>,
outer: Option<Env>,
}
impl Environment {
pub fn new_enclosed_environment(outer: &Env) -> Self {
let mut env: Environment = Default::default();
env.outer = Some(Rc::clone(outer));
env
}
pub fn get(&self, name: &str) -> Option<Rc<Object>> {
match self.store.get(name) {
Some(obj) => Some(Rc::clone(obj)),
None => {
if let Some(outer) = &self.outer {
outer.borrow().get(name)
} else {
None
}
}
}
}
pub fn set(&mut self, name: String, val: Rc<Object>) {
self.store.insert(name, val);
}
}When evaluating a function definition, you would then create a new environment that "encloses" the current one.
When looking into other ways to solve the problem, I found that this pattern isn't generally recommended since for most common use-cases you often don't need multiple mutable references to the same data. Ultimately though, it seem to be the best alternative:
Arc<Mutex<T>>: Overkill for single-threaded interpreter, andMutexis for thread safety.- Lifetime parameters: Would make the type system extremely complex, and closures need to outlive their creating scope.
Conclusion
Implementing Monkey in Rust was an incredibly rewarding experience that deepened my understanding of both language implementation and Rust's unique features. I loved the simplicity of Rust's match expressions and it's type safety was helpful in implementing error handling and understanding if my implementation was complete. My complete source code is available on GitHub and you can try out my WASM version at https://toil.ing/monkey-lang/
Whether you're learning about interpreters or exploring Rust's capabilities, I encourage you to dive in and try implementing your own version!

Member discussion