CS-7641: Machine Learning

Instructor(s): Charles Isbell / Michael Littman
Course Page: Link

CS-7641 is a core course for the OMSCS Machine Learning specialization. It serves as a introduction to three core fields of study in machine learning:

• Supervised Learning
• Unsupervised Learning
• Reinforcement Learning

Prof. Isbell takes a nuanced approach with teaching this course, emphasizing synthesis over rote memorization. As such, the course work is fairly open-ended, which allows students to demonstrate their understanding of the material. At the time of writing, the course consists of 4 major written assignments, 2 problem sets, a midterm and a final exam. The assignments are where you'll likely 90% most of your time during the course. Each assignment  requires you to experiment with various machine learning algorithms on datasets or your choosing, and for you to synthesize your learnings and insights into a a detailed paper (usually up to 10 pages). Though the rubric is hidden from students, its typically pretty fair and upfront if one completes the assigned lectures and attends office hours.

COURSE HIGHLIGHTS

With 16 weeks of course material, this course covers alot of ground. Make sure you keep up with the weekly lectures, lest you fall behind like I did! I'll try to highlight the most interesting concepts that aren't usually covered in other ML MOOCs.

Lazy Decision Trees

The most common formulation of Decision Trees you encounter are typically trained using a greedy algorithm that tries to maximize information gain with each node most commonly known as the ID3 Algorithm. It's actually entirely possible that we could develop the exact reverse of this algorithm, where instead of greedily determining the best nodes, lazily evaluate and build the tree at the point of inference. Lazy decision trees (Friedman, Kohavi & Yun 1996) have the additional benefit of making the best split for each test instance and wouldn't make unnecessary splits that a greedy algorithm would. The tradeoff, as we explored with many algorithms in this course, is this doesn't scale very well with large datasets, since each inference would require you to split over the entire dataset which would be very time or memory intensive.

Boosting RARELY overfits

One surprising result from boosted learners (where we take an ensemble of weak learners and combine their results to produce a stronger learner), is that with even with many iterations and adding alot of different learners, boosting still very rarely overfits. Although we don't go over the actual mathematical derivation of this result, Prof. Isabell explains that this results from boosting progressively increasing the error margin of already correctly labelled examples. With this tendency to maximize this margin, training accuracy will only increase.

How does the Kernel Trick work?

How do you separate non-linearly separable data with only linear separators? You map it to a higher dimensional space where you can separate them!

To avoid building an explicit map to a newer higher dimensional space, we can rely on the specific class of functions called kernel functions that can be expressed as an inner product of a lower dimensional space.

Computational Learning Theory

The most interesting section of the course was definitely learning about Probably Approximately Correct (PAC) Learning, which is a framework for defining computational complexity with machine learning. Just like in Algorithms class, we can derive bounds on an algorithms generalization error and complexity we can determine if a problem should be learnable. Generally we can define a concept class as PAC-learnable by learners L using the hypothesis class H if and only if: L will, with probability 1 − δ, output a hypothesis h ∈ H such that error D(h) ≤ ε with polynomial time and sample complexity in 1/ε, 1/δ, n (or in layman's terms, a concept is learnable if it can be learned to a reasonable degree of accuracy and within a reasonable amount of time).

We were introduced to Haussler's Theorem which provides a bound on the number of data samples you need for a problem to be PAC-learnable relative to the size of your hypothesis space:

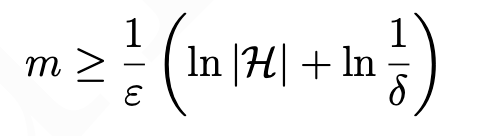
This presents a problem since most hypothesis spaces are actually infinite in size! To handle infinite spaces, we turn to the concept of Vapnik–Chervonenkis dimensions, which measures a function's ability to 'shatter' or split points. With this concept in hand, it turns out we can put a bound on sample sizes even with infinite hypothesis spaces:

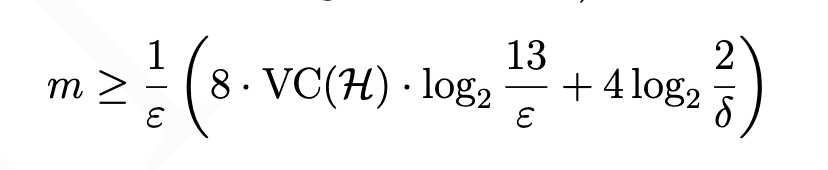
A hypothesis space H is PAC-learnable if and only if its VC dimension is finite!

Random Optimization and No Free Lunch Theorem

It can be shown that for any optimization problem, on average no other strategy is expected to do better than any other. This means that to do any better than random search, your algorithm will need have have some inherent bias that makes it more suited for that particular optimization problem.

Clustering Impossibilitiy Theorem

We can view clustering algorithms as having three fundamental properties.

• Richness - For any assignment of clusters, we can define some distance metric where that cluster can be found
• Scale Invariance - Scaling distances by a constant doesn't affect clusters
• Consistency - Shrinking or expanding distances does not change clusters

It can be shown that there exists no clustering function that can satisfy all three properties!

The BEST Classifier

For every classification problem there exists a globally optimal classifier that you can't outperform known as the Bayes Optimal Classifier? It is the classifier that has the lowest probability of misclassifying a datapoint on average. This means that no other classification method can outperform the BOC on average, with the same hypothesis space and prior knowledge! This is useful for quantifying feature importance and relevance for feature preprocessing.

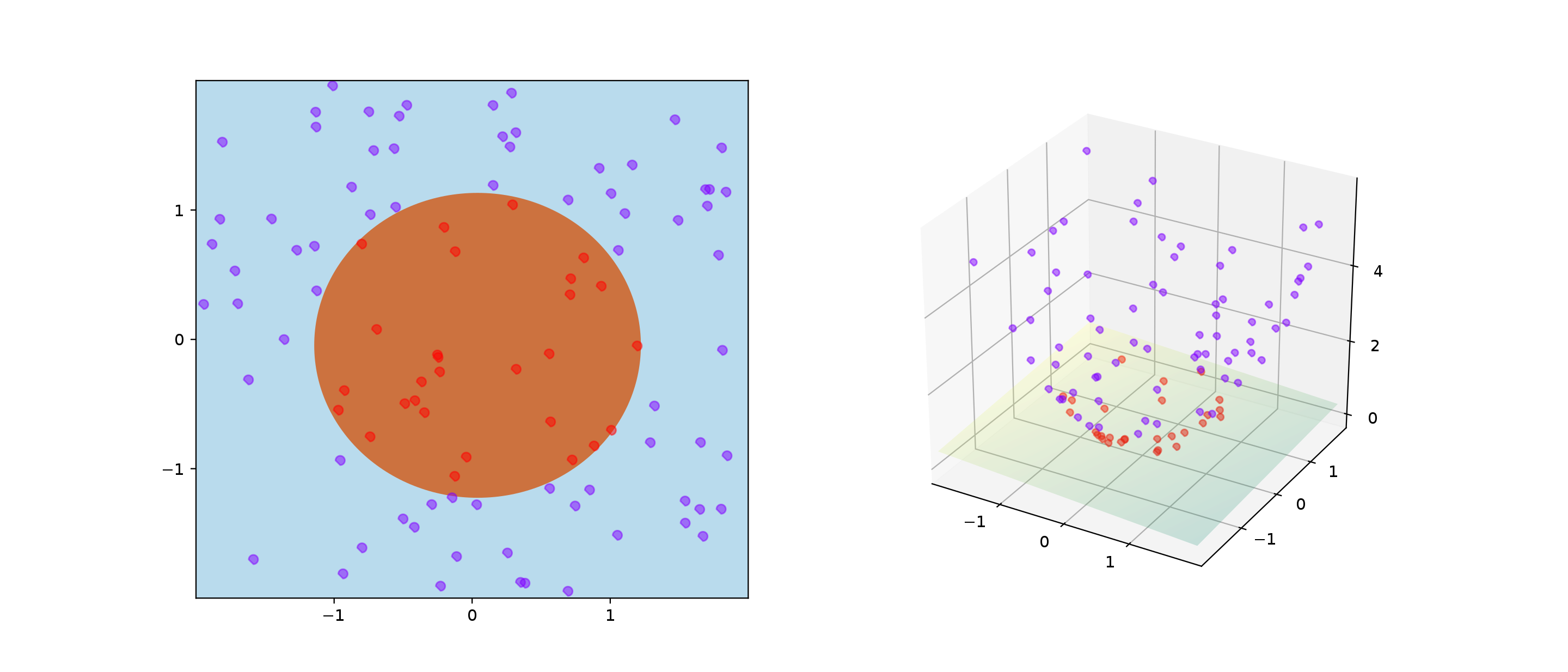
Random Projections

Randomly projecting your dataset can be just as effective as other dimensionality reduction algorithms like PCA and ICA. This is largely due to the Johnson-Lindenstrauss lemma states that large sets of vectors in a high-dimensional space can be linearly mapped in a space of much lower (but still high) dimension n with approximate preservation of distances.

Reinforcement Learning and Game Theory

I still don't fully understand these part of the lectures, but since both fields model problems as Markov Decision Processes, we can apply techinques from Reinforcement Learning, like Q-Learning onto things from Game Theory like General Sum Stochastic Games.

Conclusion

CS-7641 is a great introductory course to Machine Learning. Prof. Isbell really pushes you to truly understand the material more than just on the surface level. The written assignments force you to truy digest and synthesize the material and appreciate the core mathematical underpinnings and challenges of machine learning. If I were to summarize everything I learned in this one meme it would be: