CS-7638: Artificial Intelligence for Robotics

Instructor(s): Jay Summet / Sebastian Thrun
Course Page: Link
CS-7638 is an introductory course that covers basic techniques used in robotics. Throught its 16-week span, the instructors cover various techniques/algorithms used in the field of robotics such as:
- Bayes Filters: Histogram, Kalman & Particle Filters
- PID (Proportional–Integral–Derivative) Controllers
- Path Finding - A* and Dynamic Programming
- SLAM (Simultaneous Localization and Mapping)
Bayes Filters
We first look at the general problem of state estimation from the perspective of localization (how does a robot figure out where it is in its environment). One way to tackle this problem is to model the robot's belief in its location as a probability. The robot can model it's state belief as a probability distribution and update it over time and as it gathers measurements about it's surrounding:
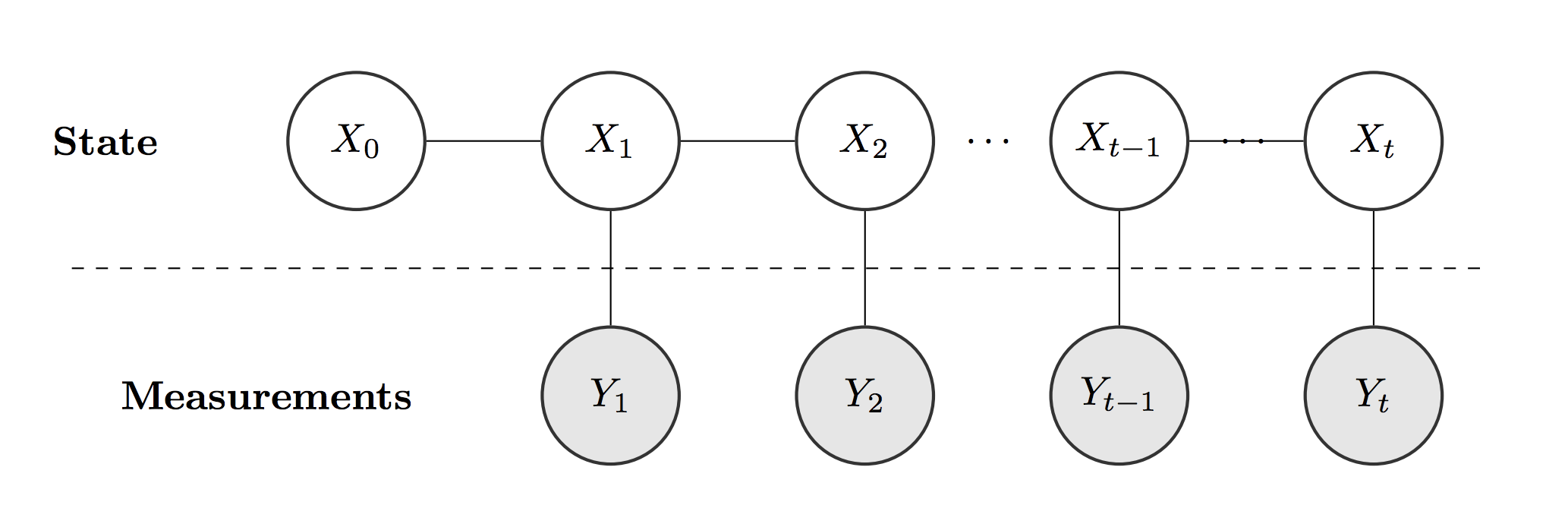
The algorithm generally becomes a matter of recursively updating it's state belief based on new control data u and measurement data z:

The challenge with implementing such an algorithm lies in modeling the beliefs and state transition probabilities. In order to make the problem tractable, we'll look at several approximations that are more easily computable, but can still effectively model the problem.
Kalman Filters
The most common and best studied approximation is the Kalman Filter. Invented by Rudolph Emil Kalman in the 1950s, Kalman Filters allow for filtering and predicting linear systems. It represents it's belief using Gaussians, which drastically improves its simplicity and computation efficiency.

The computation efficiency is mostly due to it representing it's belief by a multi-variate Gaussian distribution (a mean and uncertainty covariance). This drastically simplifies the state estimation and update step complexity, but restricts us to representing linear uni-modal states.
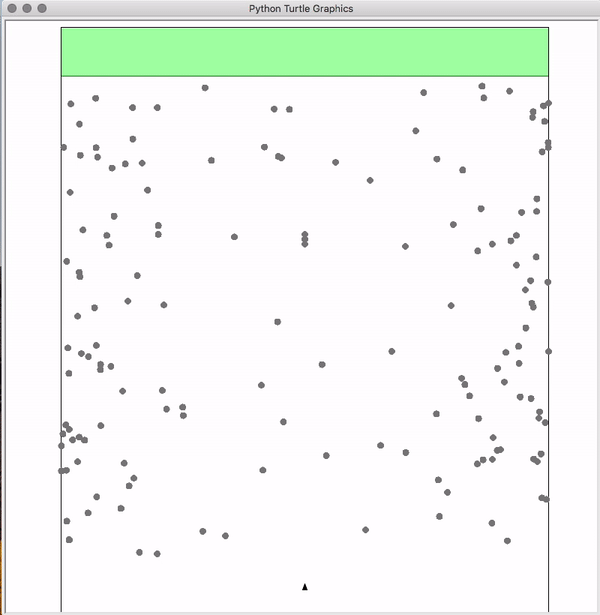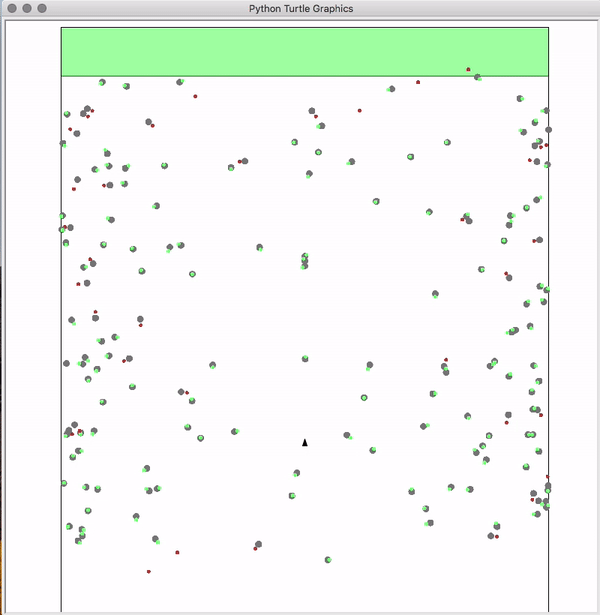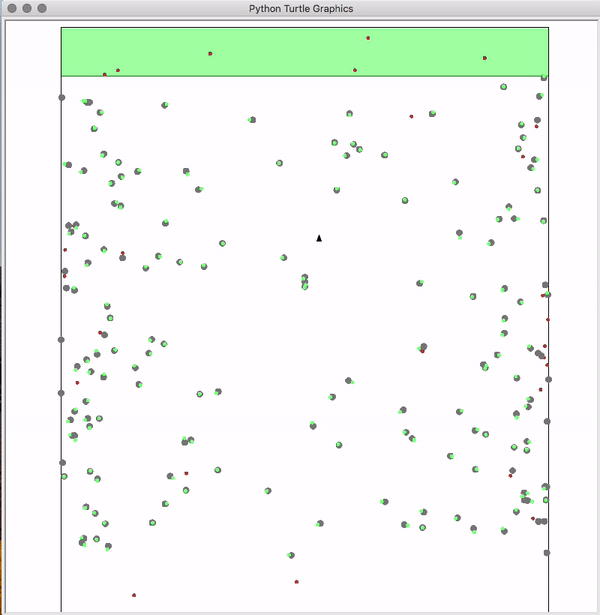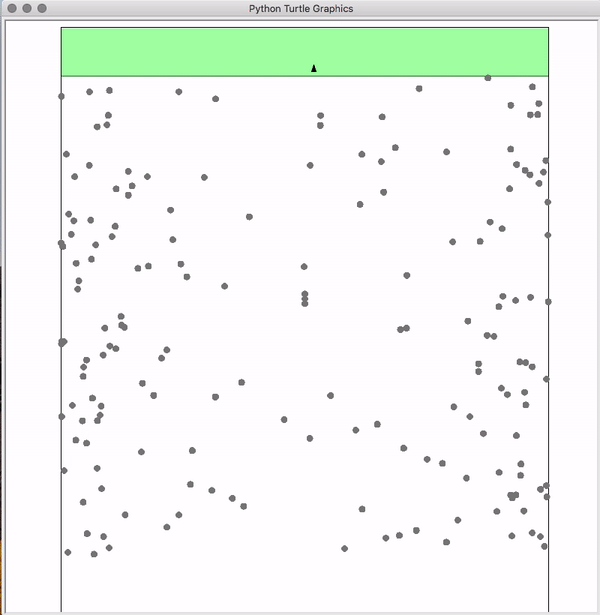
As our first coding project, we implement a 2D Kalman Filter to estimate asteroid positions, such that a spaceship could navigate to the end of a congested 2D asteroid field:
Particle Filters
Contrasting Kalman filters, there are non-parametric approaches to estimate the robot's belief state. A common approach in the field of robots is the Particle Filter, which approximates the posterior with a finite number of samples. This will never truly represent the state space, but does have the benefit of being nonparametric, and can represent a much broader selection of distributions (such as non-linear functions)

The major trick in implementing particle filters is how we perform the sampling in lines 8-11. When we retake samples to approximate the posterior, we draw samples with replacement according to an importance weight. Since the weight corresponds to the posterior probability, particles with a higher probability are more likely to be drawn. After enough iterations, the N samples we take should approximate the posterior.
For our 2nd project, we implement a 2D Particle Filter to estimate a gliders position given a terrain map and it's height. The glider can then estimate it's current position and navigate to predetermined landing location:

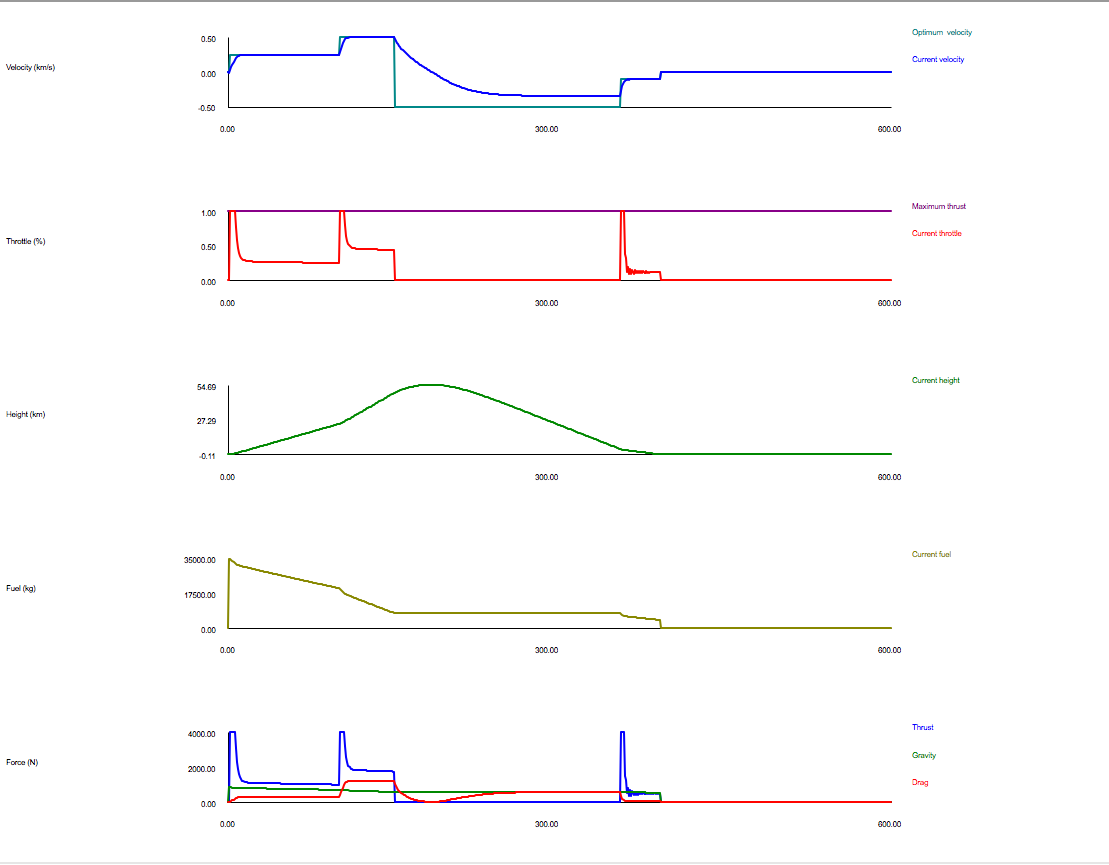
Proportional–Integral–Derivative (PID) Controllers
After exploring different implementations
of Bayes filters, the course moved onto examining control systems and methods for handling errors within a robotic control system. Sensors and actuators have error bounds and noise in their measurements and actuations, so robotics systems will typically need to employ some form of modulation/control to handle the error and move the system into its desired state. One of the most commonly used techniques is the proportional–integral–derivative controller.

A PID controller has three components:
- Proportional Error: Minimized direct error
- Integral - Measures error bias and drift accumulated over time
- Derivative - Avoids overshoot and rate of error change. Attempts to flatten the error trajectory
Tuning these three parameters in a feedback control system is typically a very powerful tool for most robotics systems and are used in applications ranging from self-driving cards, industrial engineering, temperature regulation etc...
Simultaneous Localization and Mapping (SLAM)
Nearing the end of the course, we finally look at one of the most fundamental problems in robotics, the simultaneous localization and mapping problem (SLAM). The problem happens when a robot does not have access to a map of it's environment and also doesn't have access to it's current pose/state. The robot must simultaneously acquire it's map, while also localizing itself relative to it's acquired map. Objects may be landmarks in feature-based representation, or they might be object patches detected by range finders. When an object is detected, a SLAM algorithm must reason about the relation of this object to previously detected objects. This reasoning is typically discrete: Either the object is the same as a previously detected one, or it is not.
There are various approaches to solving SLAM, such as using Kalman Filters or other Information Filters. Constraints on the robots measurements of landmarks and its current state is represented by an information matrix:
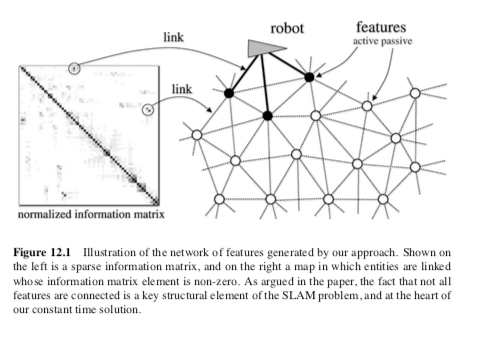
A key insight to the SLAM problem, is that the information matrix is typically very sparse and the strength and importance of a features is typically related to it's distance. This means that we could solve SLAM with an online approach where we only look at currently nearby features, which allows for a constant-time state update. As a final project, we implemented a simplified 2D version on online Graph SLAM with a robot having to pick up gems from random locations.

Overall Assessment
AI4R was my first course in the OMSCS program, and served as an easy introduction to the program and the growing field of robotics. Overall, I think I spent ~4-5 hours per week reviewing course material and working on the quizzes and assignments.
Pros:
- Interesting course content for folks that are interested in AI and Robotics
- Sebastian's lecture content was fun and engaging
- Not super-demanding in-terms of hours on assignments and quizzes
Cons:
- Course is really an introductory course, and teaches the concepts at a superficial level. Students will need to rely on the textbook if they want a more rigorous mathematical derivations of each algorithm
In summary, this was an amazing introductory course for anyone just starting on their OMSCS journey and a great way to dive into the world of Artificial Intelligence and Robotics.