Towers of Hanoi

An age-old puzzle that's challenged kids and pancake chefs for ages:
The goal of the puzzle is to move an entire stack of disks from one rod/plate to another with the following restrictions:
- Only one disk can be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack
- No disk may be placed on top of a smaller disk.
So how can we go about solving this programatically? The key insight is that this problem has optimal substructure. This means that the solution for a larger problem, say for 4 disks is composed of the solutions for smaller subproblems: 1,2 and 3 disks.
def moveTower(height,fromPole, toPole, withPole):
if height >= 1:
moveTower(height-1,fromPole,withPole,toPole)
moveDisk(fromPole,toPole)
moveTower(height-1,withPole,toPole,fromPole)
def moveDisk(fp,tp):
print("moving disk from",fp,"to",tp)
moveTower(3,"A","B","C")
We first move the first n-1 disks from pole A to B by calling moveTower recursively but for the stack of n-1 disks. Then we can move disk n from pole A to C. We can then do the same recurisive call and move the n-1 disks from B to C.
The recursive solution seems a bit expensive, with the two recursive calls leading to a $O(2^n)$ runtime. Can we do a bit better?
Top-Down Memoization
Our recursive search right now is solving the same subproblem over and over again. If we saved or memoized the result, we could possibly trade off some of our runtime by using more memory and essentially caching the solutions to each subproblem.
memo = []
lookup = ["ABC","ACB","BAC","BCA","CAB","CBA"]
def topDown(height,fromPole, toPole, withPole):
global memo
memo = [[-1 for x in range(6)] for y in range(height+1)]
memo[0][0] = ""
for x in range(6):
memo[0][x] = ""
return topDownHelper(height,fromPole, toPole, withPole)
def topDownHelper(height,fromPole, toPole, withPole):
global memo
move = fromPole + toPole + withPole
index = 0
while move != lookup[index]:
index += 1
if memo[height][index] < 0:
memo[height][index] = topDownHelper(height-1,fromPole,withPole,toPole)\
+ fromPole +'->'+ toPole +', ' \
+ topDownHelper(height-1,withPole,toPole,fromPole)
return memo[height][index]
print topDown(3,"A","B","C")
Bottom-up Dynamic Programming
Another approach would be to intelligently build up our solution, solving for 1 disk, then 2 disks, etc... By going in the opposite direction of our recursive solution, we save time by not solving the same subproblems. This is a technique dubbed dynamic programming. Since we are building up our solution successively, we only need to remember the solutions that are needed immediately. This saves us some valuable space.
moves = ["A->B","A->C","B->A","B->C","C->A","C->B"]
prevLookup = [1,0,3,2,5,4]
prev2Lookup = [5,3,4,1,2,0]
def bottomUp(height,fromPole, toPole, withPole):
prev = ["" for x in range(6)]
curr = ["" for x in range(6)]
for i in range(height):
for j in range(len(moves)):
prevStr = prev[prevLookup[j]] + ', ' if prev[prevLookup[j]] != "" else ""
nextStr = ', ' + prev[prev2Lookup[j]] if prev[prev2Lookup[j]] != "" else ""
curr[j] = prevStr + moves[j] + nextStr
curr,prev = prev,curr
return prev
print bottomUp(4,"A","B","C")[0]
Performance
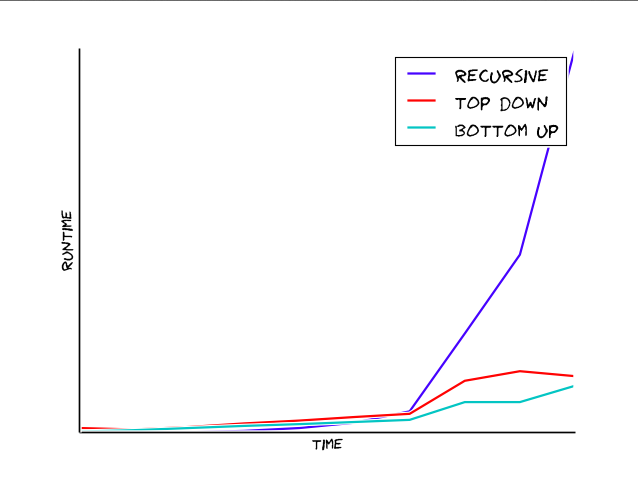
Doing a quick check on each implementation's running time, we see that the recursive solution explodes exponentially, while our memoized/dynamic programming implementations grow linearly. Clearly dynamic programming is the way to go!